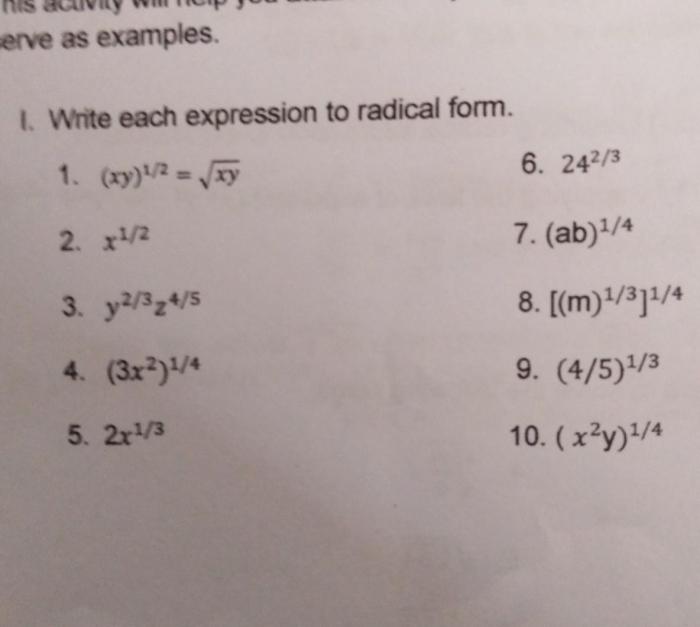Radical Functions and Rational Exponents Unit Test Part 1 delves into the fundamental concepts of radical functions and rational exponents, providing a thorough assessment of students’ understanding of these mathematical operations. This unit test serves as a valuable tool for educators to evaluate students’ proficiency in simplifying expressions, identifying domains and ranges, and applying properties related to radicals and rational exponents.

Radical Functions and Rational Exponents Unit Test Part 1

This unit test assesses students’ understanding of radical functions and rational exponents, which are fundamental concepts in mathematics. The test includes questions that cover the definition, properties, domain, and range of radical functions, as well as the definition, simplification, and properties of rational exponents.

1. Radical Functions

Radical functions are functions that involve square roots or other radical expressions. They are defined as follows:

• A radical function is a function of the form f(x) = √(ax + b), where a and b are constants and a ≠ 0.
• The domain of a radical function is the set of all values of x for which the expression inside the radical is non-negative.
• The range of a radical function is the set of all values of f(x) that can be obtained for all values of x in the domain.

Radical functions have several important properties, including:

• They are continuous for all values of x in their domain.
• They are differentiable for all values of x in their domain except for x = -b/a.
• Their graphs are typically smooth and have a V-shape.

Here are some examples of radical functions:

• f(x) = √x
• f(x) = √(x + 2)
• f(x) = √(x^2 – 4)

2. Rational Exponents, Radical functions and rational exponents unit test part 1

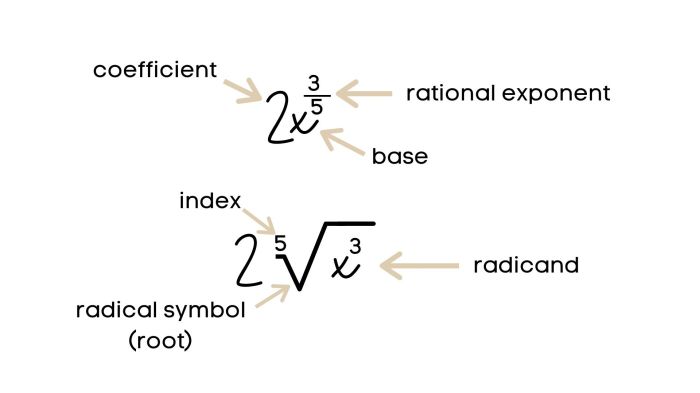
Rational exponents are exponents that are expressed as fractions. They are defined as follows:

• A rational exponent is an exponent of the form m/n, where m and n are integers and n ≠ 0.
• The expression x^(m/n) is equivalent to the nth root of x^m.

Rational exponents have several important properties, including:

• (x^a)^b = x^(a*b)
• x^(a/b) = √(x^a)
• (x*y)^a = x^a – y^a
• (x/y)^a = x^a / y^a

Quick FAQs

What is the purpose of Radical Functions and Rational Exponents Unit Test Part 1?

Radical Functions and Rational Exponents Unit Test Part 1 is designed to evaluate students’ understanding of radical functions and rational exponents, ensuring their proficiency in simplifying expressions, identifying domains and ranges, and applying relevant properties.

What types of questions are included in the unit test?

The unit test encompasses a variety of question formats, including multiple choice, short answer, and problem-solving tasks. These questions assess students’ comprehension of radical functions and rational exponents at varying difficulty levels.

How can students prepare for the unit test?

To prepare for the unit test, students are encouraged to thoroughly review their class notes, textbooks, and any additional study materials provided by their instructor. Additionally, practicing sample problems and seeking clarification on challenging concepts can enhance their understanding and readiness for the assessment.